This post shows how filling histograms can be done in very different ways thereby connecting very different areas: from gradient boosted trees to SQL queries to one-hot encoding. Let’s jump into it!
Modern gradient boosted trees (GBT) like LightGBM, XGBoost and the HistGradientBoostingRegressor of scikit-learn all use two techniques on top of standard gradient boosting:
- 2nd order Taylor expansion of the loss which amounts to using gradients and hessians.
- One histogram per feature: bin the feature and fill the histogram with the gradients and hessians.
The filling of the histograms is often the bottleneck when fitting GBTs. While filling a single histogram is very fast, this operation is executed many times: for each boosting round, for each tree split and for each feature. This is the reason why GBT implementations have dedicated routines for it. We look into this operation from different angles.
For the coming (I)Python code snippets to work (# %% indicates a new notebook cell), we need the following imports.
import duckdb # v0.5.1
import matplotlib.pyplot as plt # v.3.6.1
from matplotlib.ticker import MultipleLocator
import numpy as np # v1.23.4
import pandas as pd # v1.5.0
import pyarrow as pa # v9.0.0
import tabmat # v3.1.2
from sklearn.ensemble._hist_gradient_boosting.histogram import (
_build_histogram_root,
) # v1.1.2
from sklearn.ensemble._hist_gradient_boosting.common import (
HISTOGRAM_DTYPE
)Naive Histogram Visualisation
As a starter, we create a small table with two columns: bin index and value of the hessian.
def highlight(df):
if df["bin"] == 0:
return ["background-color: rgb(255, 128, 128)"] * len(df)
elif df["bin"] == 1:
return ["background-color: rgb(128, 255, 128)"] * len(df)
else:
return ['background-color: rgb(128, 128, 255)'] * len(df)
df = pd.DataFrame({"bin": [0, 2, 1, 0, 1], "hessian": [1.5, 1, 2, 2.5, 3]})
df.style.apply(highlight, axis=1)| bin | hessian | |
|---|---|---|
| 0 | 0 | 1.500000 |
| 1 | 2 | 1.000000 |
| 2 | 1 | 2.000000 |
| 3 | 0 | 2.500000 |
| 4 | 1 | 3.000000 |
A histogram then sums up all the hessian values belonging to the same bin. The result looks like the following.
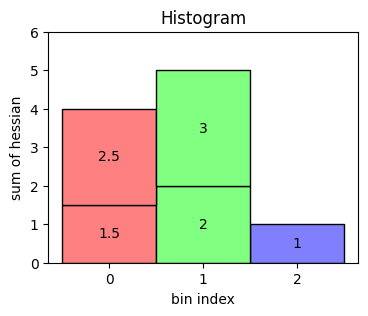
Dedicated Method
We simulate filling the histogram of a single feature. Therefore, we draw 1,000,000 random variables for gradients and hessians as well as the bin indices.
import duckdb
import pyarrow as pa
import numpy as np
import tabmat
from sklearn.ensemble._hist_gradient_boosting.histogram import (
_build_histogram_root,
)
from sklearn.ensemble._hist_gradient_boosting.common import HISTOGRAM_DTYPE
rng = np.random.default_rng(42)
n_obs = 1000_000
n_bins = 256
binned_feature = rng.integers(0, n_bins, size=n_obs, dtype=np.uint8)
gradients = rng.normal(size=n_obs).astype(np.float32)
hessians = rng.lognormal(size=n_obs).astype(np.float32)Now we use the dedicated (and private!) and single-threaded method _build_histogram_root from sckit-learn to fill a histogram.
hist_root = np.zeros((1, n_bins), dtype=HISTOGRAM_DTYPE) %time _build_histogram_root(0, binned_feature, gradients, hessians, hist_root) # Wall time: 1.38 ms
This executes in around 1.4 ms. This is quite fast. But again, imagine 100 boosting rounds with 10 tree splits on average and 100 features. This means this is done around 100,000 times and would therefore take roughly 2 minutes.
Let’s have a look at the first 5 bins:
hist_root[:, 0:5]
array([[(-79.72386998, 6508.89500265, 3894),
( 37.98393589, 6460.63222205, 3998),
( 53.54256977, 6492.22722797, 3805),
( 21.19542398, 6797.34159299, 3928),
( 16.24716742, 6327.03757573, 3875)]],
dtype=[('sum_gradients', '<f8'), ('sum_hessians', '<f8'), ('count', '<u4')])SQL Group-By Query
Someone familiar with SQL and database queries might immediately see how this task can be formulated as SQL group-by-aggregate query. To demonstrate it on our simulated data, we use DuckDB as well as Apache Arrow (the file format as well as the Python library pyarrow). You can read more about DuckDB in our post DuckDB: Quacking SQL.
# %%
con = duckdb.connect()
arrow_table = pa.Table.from_pydict(
{
"bin": binned_feature,
"gradients": gradients,
"hessians": hessians,
})
# Read data once to make timing fairer
arrow_result = con.execute("SELECT * FROM arrow_table")
# %%
%%time
arrow_result = con.execute("""
SELECT
bin as bin,
SUM(gradients) as sum_gradients,
SUM(hessians) as sum_hessians,
COUNT() as count
FROM arrow_table
GROUP BY bin
""").arrow()
# Wall time: 6.52 msOn my laptop, this takes about 6.5 ms and, upon sorting, gives the same results:
arrow_result.sort_by("bin").slice(length=5)pyarrow.Table bin: uint8 sum_gradients: double sum_hessians: double count: int64 ---- bin: [[0,1,2,3,4]] sum_gradients: [[-79.72386997545254,37.98393589106854,53.54256977112527,21.195423980039777,16.247167424764484]] sum_hessians: [[6508.895002648234,6460.632222048938,6492.227227974683,6797.341592986137,6327.037575732917]] count: [[3894,3998,3805,3928,3875]]
As we have the table as an Arrow table, we can stay within pyarrow:
%%time
arrow_result = arrow_table.group_by("bin").aggregate(
[
("gradients", "sum"),
("hessians", "sum"),
("bin", "count"),
]
)
# Wall time: 10.8 msThe fact that DuckDB is faster than Arrow on this task might have to do with the large invested effort on parallelised group-by operations, see their post Parallel Grouped Aggregation in DuckDB for more infos.
One-Hot encoded Matrix Multiplication
I think it is very interesting that filling histograms can be written as a matrix multiplication! The trick is to view the feature as a categorical feature and use its one-hot encoded matrix representation. This blows up memory, of course. Note that one-hot encoding is usually met with generalized linear models (GLM) in order to incorporate nominal categorical feature variables with no internal ordering in the design matrix.
For our demonstration, we use a numpy index trick to construct the one-hot encoded matrix employing the fact that the binned feature already contains the right indices.
# %% %%time m_OHE = np.eye(n_bins)[binned_feature].T vec = np.column_stack((gradients, hessians, np.ones_like(gradients))) # Wall time: 770 ms # %% %time result_ohe = m_OHE @ vec # Wall time: 199 ms # %% result_ohe[:5]
array([[ -79.72386998, 6508.89500265, 3894. ],
[ 37.98393589, 6460.63222205, 3998. ],
[ 53.54256977, 6492.22722797, 3805. ],
[ 21.19542398, 6797.34159299, 3928. ],
[ 16.24716742, 6327.03757573, 3875. ]])This is way slower, but, somehow surprisingly, produces the same result.
The one-hot encoded matrix is very sparse, with only one non-zero value per column, i.e. only one out of 256 (number of bins) values is non-zero. This structure can be exploited to reduce both CPU time as well as memory consumption, with the help of the package tabmat that was built to accelerate GLMs. Unfortunately, tabmat only provides a matrix-vector multiplication (and the sandwich product, of course), but no matrix-matrix multiplication. So we have to do a little extra work.
# %%
%time m_categorical = tabmat.CategoricalMatrix(cat_vec=binned_feature)
# Wall time: 21.5 ms
# %%
# tabmat needs contigous arrays with dtype = Python float = float64
vec = np.asfortranarray(vec, dtype=float)
# %%
%%time
tabmat_result = np.column_stack(
(
vec[:, 0] @ m_categorical,
vec[:, 1] @ m_categorical,
vec[:, 2] @ m_categorical,
)
)
# Wall time: 4.82 ms
# %%
tabmat_result[0:5]array([[ -79.72386998, 6508.89500265, 3894. ],
[ 37.98393589, 6460.63222205, 3998. ],
[ 53.54256977, 6492.22722797, 3805. ],
[ 21.19542398, 6797.34159299, 3928. ],
[ 16.24716742, 6327.03757573, 3875. ]])While the timing of this approach is quite good, the construction of a CategoricalMatrix requires more time than the matrix-vector multiplication.
Conclusion
In the end, the special (Cython) routine of scikit-learn ist the fastest of our tested methods for filling histograms. The other GBT libraries have their own even more specialised routines which might be a reason for even faster fit times. What we learned in this post is that this seemingly simple task plays a very crucial part in modern GBTs and can be accomplished by very different approaches. These different approaches uncover connections of algorithms of quite different domains.
The full code as ipython notebook can be found at https://github.com/lorentzenchr/notebooks/blob/master/blogposts/2022-10-31%20histogram-GBT-GroupBy-OHE.ipynb.