This question sends shivers down the poor modelers spine…
The {hstats} R package introduced in our last post measures their strength using Friedman’s H-statistics, a collection of statistics based on partial dependence functions.
On Github, the preview version of {hstats} 1.0.0 out – I will try to bring it to CRAN in about one week (October 2023). Until then, try it via devtools::install_github("mayer79/hstats")
The current version offers:
- H statistics per feature, feature pair, and feature triple
- Multivariate predictions at no additional cost
- A convenient API
- Other important tools from explainable ML:
- performance calculations
- permutation importance (e.g., to select features for calculating H-statistics)
- partial dependence plots (including grouping, multivariate, multivariable)
- individual conditional expectations (ICE)
- Case-weights are available for all methods, which is important, e.g., in insurance applications
- The option for fast quantile approximation of H-statistics
This post has two parts:
- Example with house-prices and XGBoost
- Naive benchmark against {iml}, {DALEX}, and my old {flashlight}.
1. Example
Let’s model logarithmic sales prices of houses sold in Miami Dade County, a dataset prepared by Prof. Dr. Steven Bourassa, and available in {shapviz}. We use XGBoost with interaction constraints to provide a model additive in all structure information, but allowing for interactions between latitude/longitude for a flexible representation of geographic effects.
The following code prepares the data, splits the data into train and validation, and then fits an XGBoost model.
library(hstats)
library(shapviz)
library(xgboost)
library(ggplot2)
# Data preparation
colnames(miami) <- tolower(colnames(miami))
miami <- transform(miami, log_price = log(sale_prc))
x <- c("tot_lvg_area", "lnd_sqfoot", "latitude", "longitude",
"structure_quality", "age", "month_sold")
coord <- c("longitude", "latitude")
# Modeling
set.seed(1)
ix <- sample(nrow(miami), 0.8 * nrow(miami))
train <- data.frame(miami[ix, ])
valid <- data.frame(miami[-ix, ])
y_train <- train$log_price
y_valid <- valid$log_price
X_train <- data.matrix(train[x])
X_valid <- data.matrix(valid[x])
dtrain <- xgb.DMatrix(X_train, label = y_train)
dvalid <- xgb.DMatrix(X_valid, label = y_valid)
ic <- c(
list(which(x %in% coord) - 1),
as.list(which(!x %in% coord) - 1)
)
# Fit via early stopping
fit <- xgb.train(
params = list(
learning_rate = 0.15,
objective = "reg:squarederror",
max_depth = 5,
interaction_constraints = ic
),
data = dtrain,
watchlist = list(valid = dvalid),
early_stopping_rounds = 20,
nrounds = 1000,
callbacks = list(cb.print.evaluation(period = 100))
)Now it is time for a compact analysis with {hstats} to interpret the model:
average_loss(fit, X = X_valid, y = y_valid) # 0.0247 MSE -> 0.157 RMSE
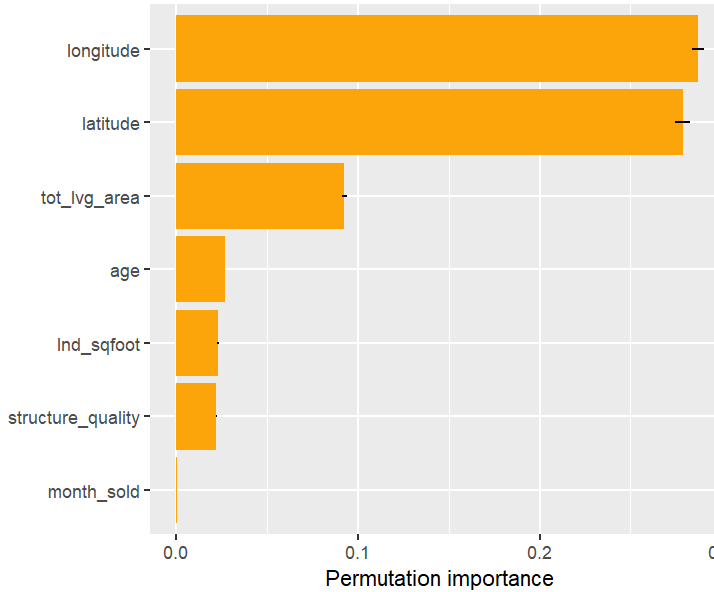
perm_importance(fit, X = X_valid, y = y_valid) |>
plot()
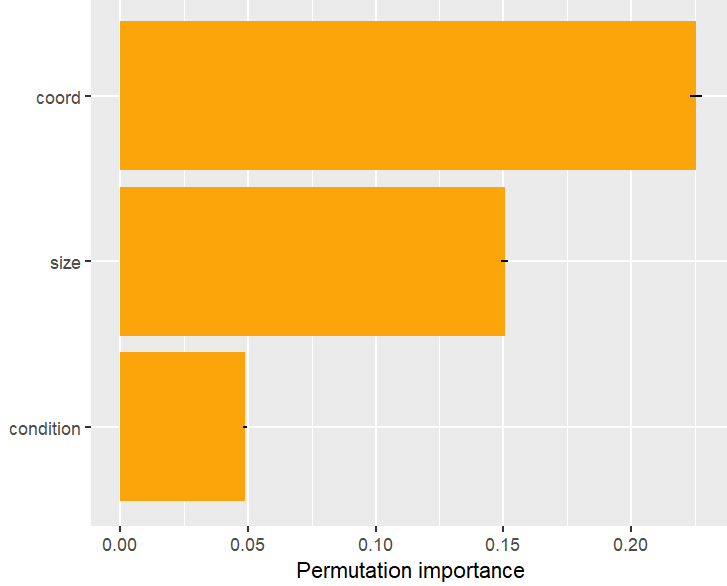
# Or combining some features
v_groups <- list(
coord = c("longitude", "latitude"),
size = c("lnd_sqfoot", "tot_lvg_area"),
condition = c("age", "structure_quality")
)
perm_importance(fit, v = v_groups, X = X_valid, y = y_valid) |>
plot()
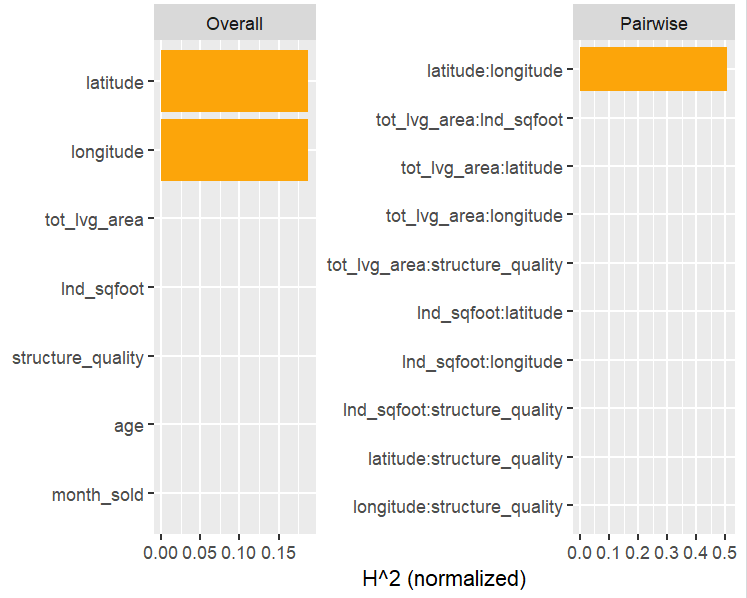
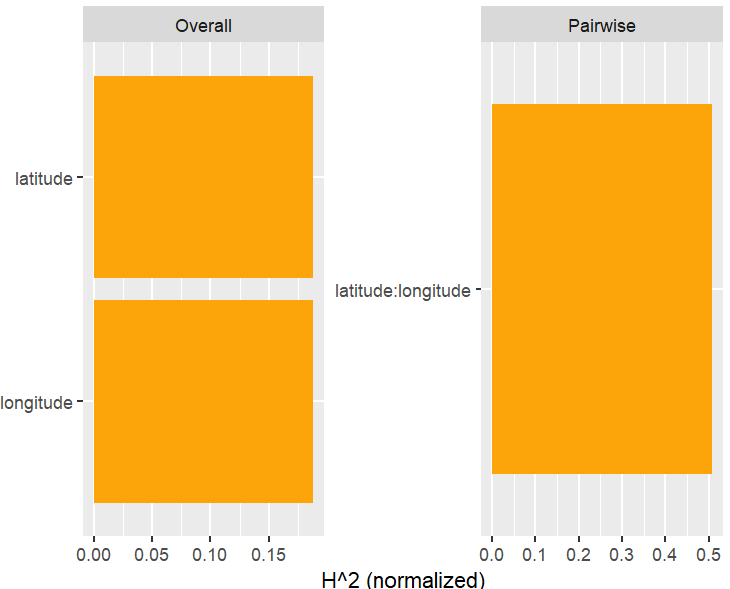
H <- hstats(fit, v = x, X = X_valid)
H
plot(H)
plot(H, zero = FALSE)
h2_pairwise(H, zero = FALSE, squared = FALSE, normalize = FALSE)
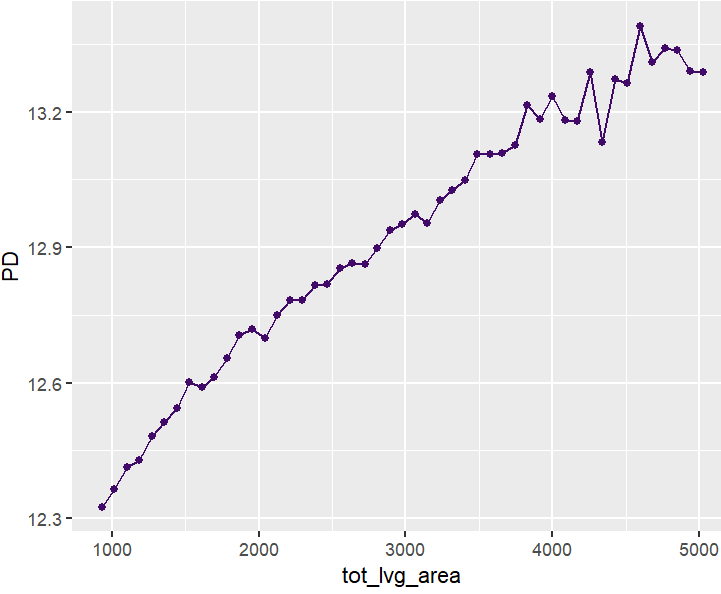
partial_dep(fit, v = "tot_lvg_area", X = X_valid) |>
plot()
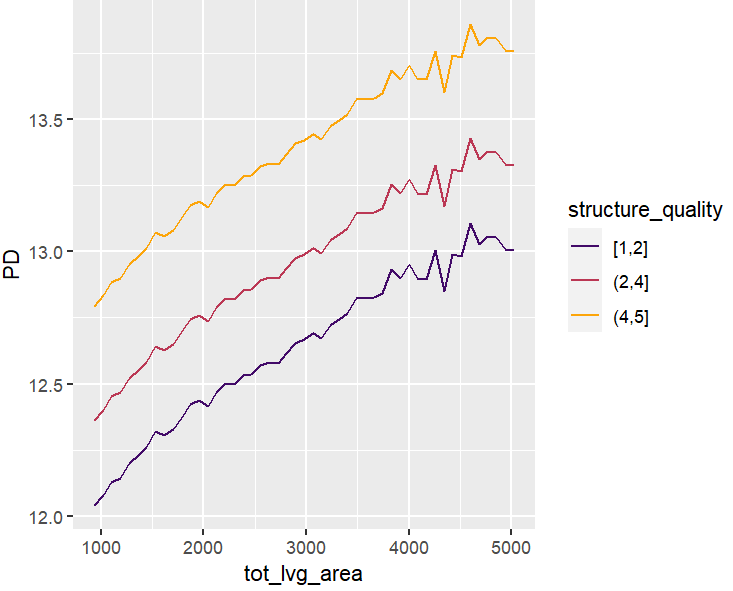
partial_dep(fit, v = "tot_lvg_area", X = X_valid, BY = "structure_quality") |>
plot(show_points = FALSE)
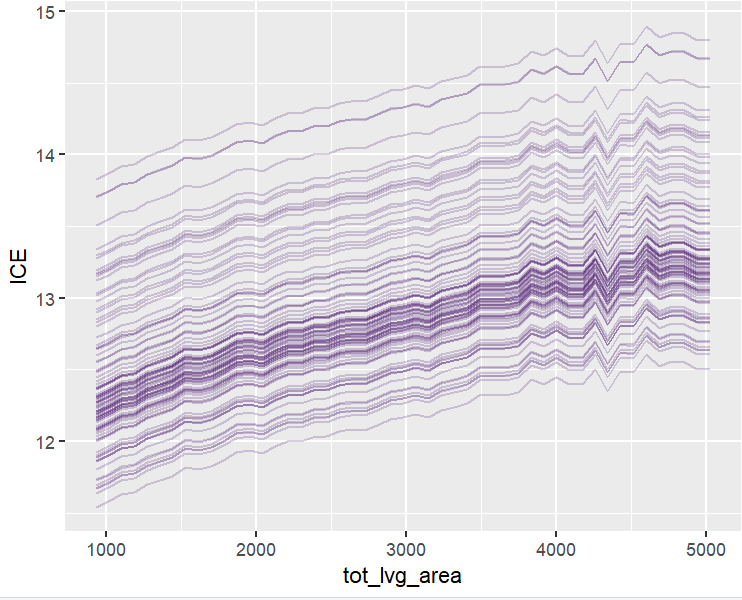
plot(ii <- ice(fit, v = "tot_lvg_area", X = X_valid))
plot(ii, center = TRUE)
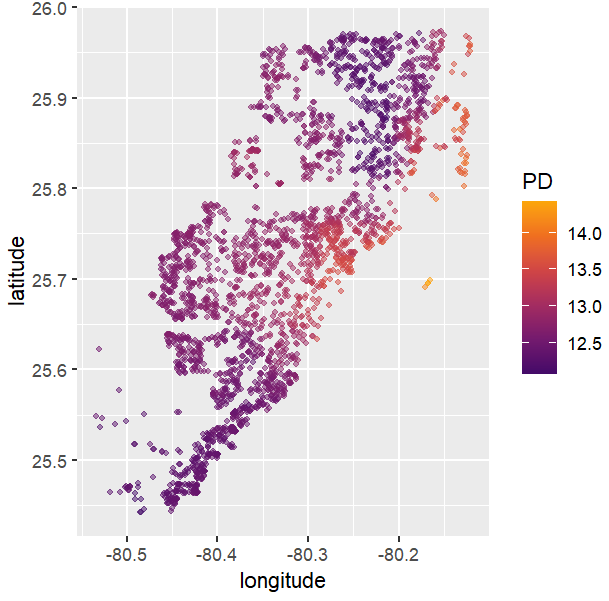
# Spatial plots
g <- unique(X_valid[, coord])
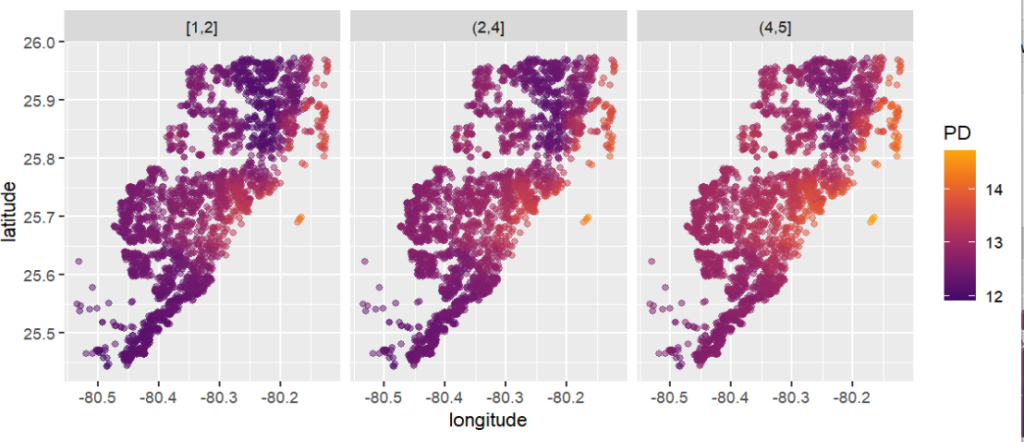
pp <- partial_dep(fit, v = coord, X = X_valid, grid = g)
plot(pp, d2_geom = "point", alpha = 0.5, size = 1) +
coord_equal()
# Takes some seconds because it generates the last plot per structure quality
partial_dep(fit, v = coord, X = X_valid, grid = g, BY = "structure_quality") |>
plot(pp, d2_geom = "point", alpha = 0.5) +
coord_equal()
)Results summarized by plots
Permutation importance
H-Statistics
Let’s now move on to interaction statistics.

PDPs and ICEs
Naive Benchmark
All methods in {hstats} are optimized for speed. But how fast are they compared to other implementations? Note that: this is just a simple benchmark run on a Windows notebook with Intel i7-8650U CPU.
Note that {iml} offers a parallel backend, but we could not make it run with XGBoost and Windows. Let me know how fast it is using parallelism and Linux!
Setup + benchmark on permutation importance
Always using the full validation dataset and 10 repetitions.
library(iml) # Might benefit of multiprocessing, but on Windows with XGB models, this is not easy
library(DALEX)
library(ingredients)
library(flashlight)
library(bench)
set.seed(1)
# iml
predf <- function(object, newdata) predict(object, data.matrix(newdata[x]))
mod <- Predictor$new(fit, data = as.data.frame(X_valid), y = y_valid,
predict.function = predf)
# DALEX
ex <- DALEX::explain(fit, data = X_valid, y = y_valid)
# flashlight (my slightly old fashioned package)
fl <- flashlight(
model = fit, data = valid, y = "log_price", predict_function = predf, label = "lm"
)
# Permutation importance: 10 repeats over full validation data (~2700 rows)
bench::mark(
iml = FeatureImp$new(mod, n.repetitions = 10, loss = "mse", compare = "difference"),
dalex = feature_importance(ex, B = 10, type = "difference", n_sample = Inf),
flashlight = light_importance(fl, v = x, n_max = Inf, m_repetitions = 10),
hstats = perm_importance(fit, X = X_valid, y = y_valid, m_rep = 10, verbose = FALSE),
check = FALSE,
min_iterations = 3
)
# expression min median `itr/sec` mem_alloc `gc/sec` n_itr n_gc total_time
# iml 1.58s 1.58s 0.631 209.4MB 2.73 3 13 4.76s
# dalex 566.21ms 586.91ms 1.72 34.6MB 0.572 3 1 1.75s
# flashlight 587.03ms 613.15ms 1.63 27.1MB 1.63 3 3 1.84s
# hstats 353.78ms 360.57ms 2.79 27.2MB 0 3 0 1.08s{hstats} is about 30% faster as the second, {DALEX}.
Partial dependence
Here, we study the time for crunching partial dependence of a continuous feature and a discrete feature.
# Partial dependence (cont) v <- "tot_lvg_area" bench::mark( iml = FeatureEffect$new(mod, feature = v, grid.size = 50, method = "pdp"), dalex = partial_dependence(ex, variables = v, N = Inf, grid_points = 50), flashlight = light_profile(fl, v = v, pd_n_max = Inf, n_bins = 50), hstats = partial_dep(fit, v = v, X = X_valid, grid_size = 50, n_max = Inf), check = FALSE, min_iterations = 3 ) # expression min median `itr/sec` mem_alloc `gc/sec` n_itr n_gc total_time # iml 1.11s 1.13s 0.887 376.3MB 3.84 3 13 3.38s # dalex 782.13ms 783.08ms 1.24 192.8MB 2.90 3 7 2.41s # flashlight 367.73ms 372.5ms 2.68 67.9MB 2.68 3 3 1.12s # hstats 220.88ms 222.5ms 4.50 14.2MB 0 3 0 666.33ms # Partial dependence (discrete) v <- "structure_quality" bench::mark( iml = FeatureEffect$new(mod, feature = v, method = "pdp", grid.points = 1:5), dalex = partial_dependence(ex, variables = v, N = Inf, variable_type = "categorical", grid_points = 5), flashlight = light_profile(fl, v = v, pd_n_max = Inf), hstats = partial_dep(fit, v = v, X = X_valid, n_max = Inf), check = FALSE, min_iterations = 3 ) # expression min median `itr/sec` mem_alloc `gc/sec` n_itr n_gc total_time # iml 90ms 96ms 10.6 13.29MB 7.06 3 2 283ms # dalex 170.6ms 174.4ms 5.73 20.55MB 2.87 2 1 349ms # flashlight 40.8ms 43.8ms 23.1 6.36MB 2.10 11 1 476ms # hstats 23.5ms 24.4ms 40.6 1.53MB 2.14 19 1 468ms
{hstats} is 1.5 to 2 times faster than {flashlight}, and about four times as fast as the other packages. It’s memory foodprint is much lower.
H-statistics
How fast can overall H-statistics be computed? How fast can it do pairwise calculations?
{DALEX} does not offer these statistics yet. {iml} was the first model-agnostic implementation of H-statistics I am aware of. It uses quantile approximation by default, but we purposely force it to calculate exact, in order to compare the numbers. Thus, we made it slower than it actually is.
# H-Stats -> we use a subset of 500 rows
X_v500 <- X_valid[1:500, ]
mod500 <- Predictor$new(fit, data = as.data.frame(X_v500), predict.function = predf)
fl500 <- flashlight(fl, data = as.data.frame(valid[1:500, ]))
# iml # 225s total, using slow exact calculations
system.time( # 90s
iml_overall <- Interaction$new(mod500, grid.size = 500)
)
system.time( # 135s for all combinations of latitude
iml_pairwise <- Interaction$new(mod500, grid.size = 500, feature = "latitude")
)
# flashlight: 14s total, doing only one pairwise calculation, otherwise would take 63s
system.time( # 12s
fl_overall <- light_interaction(fl500, v = x, grid_size = Inf, n_max = Inf)
)
system.time( # 2s
fl_pairwise <- light_interaction(
fl500, v = coord, grid_size = Inf, n_max = Inf, pairwise = TRUE
)
)
# hstats: 3s total
system.time({
H <- hstats(fit, v = x, X = X_v500, n_max = Inf)
hstats_overall <- h2_overall(H, squared = FALSE, zero = FALSE)
hstats_pairwise <- h2_pairwise(H, squared = FALSE, zero = FALSE)
}
)
# Overall statistics correspond exactly
iml_overall$results |> filter(.interaction > 1e-6)
# .feature .interaction
# 1: latitude 0.2458269
# 2: longitude 0.2458269
fl_overall$data |> subset(value > 0, select = c(variable, value))
# variable value
# 1 latitude 0.246
# 2 longitude 0.246
hstats_overall
# longitude latitude
# 0.2458269 0.2458269
# Pairwise results match as well
iml_pairwise$results |> filter(.interaction > 1e-6)
# .feature .interaction
# 1: longitude:latitude 0.3942526
fl_pairwise$data |> subset(value > 0, select = c(variable, value))
# latitude:longitude 0.394
hstats_pairwise
# latitude:longitude
# 0.3942526 - {hstats} is about four times as fast as {flashlight}.
- Since one often want to study relative and absolute H-statistics, in practice, the speed-up would be about a factor of eight.
- In multi-classification/multi-output settings with m categories, the speed-up would be even m times larger.
- The fast approximation via quantile binning is again a factor of four faster. The difference would diminish if we would calculate many pairwise or three-way H-statistics.
- Forcing all three packages to calculate exact statistics, all results match.
Wrap-Up
- {hstats} is much faster than other XAI packages, at least in our use-case. This includes H-statistics, permutation importance, and partial dependence. Note that making good benchmarks is not my strength, so forgive any bias in the results.
- The memory foodprint is lower as well.
- With multivariate output, the potential is even larger.
- H-Statistics match other implementations.
Try it out!
The full R code in one piece is here.
Leave a Reply