Within only a few years, SHAP (Shapley additive explanations) has emerged as the number 1 way to investigate black-box models. The basic idea is to decompose model predictions into additive contributions of the features in a fair way. Studying decompositions of many predictions allows to derive global properties of the model.
What happens if we apply SHAP algorithms to additive models? Why would this ever make sense?
In the spirit of our “Lost In Translation” series, we provide both high-quality Python and R code.
The models
Let’s build the models using a dataset with three highly correlated covariates and a (deterministic) response.
library(lightgbm)
library(kernelshap)
library(shapviz)
#===================================================================
# Make small data
#===================================================================
make_data <- function(n = 100) {
x1 <- seq(0.01, 1, length = n)
data.frame(
x1 = x1,
x2 = log(x1),
x3 = x1 > 0.7
) |>
transform(y = 1 + 0.2 * x1 + 0.5 * x2 + x3 + sin(2 * pi * x1))
}
df <- make_data()
head(df)
cor(df) |>
round(2)
# x1 x2 x3 y
# x1 1.00 0.90 0.80 0.46
# x2 0.90 1.00 0.58 0.58
# x3 0.80 0.58 1.00 0.51
# y 0.46 0.58 0.51 1.00
#===================================================================
# Additive linear model and additive boosted trees
#===================================================================
# Linear regression
fit_lm <- lm(y ~ poly(x1, 3) + poly(x2, 3) + x3, data = df)
summary(fit_lm)
# Boosted trees
xvars <- setdiff(colnames(df), "y")
X <- data.matrix(df[xvars])
params <- list(
learning_rate = 0.05,
objective = "mse",
max_depth = 1,
colsample_bynode = 0.7
)
fit_lgb <- lgb.train(
params = params,
data = lgb.Dataset(X, label = df$y),
nrounds = 300
)import numpy as np
import lightgbm as lgb
import shap
from sklearn.preprocessing import PolynomialFeatures
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
#===================================================================
# Make small data
#===================================================================
def make_data(n=100):
x1 = np.linspace(0.01, 1, n)
x2 = np.log(x1)
x3 = x1 > 0.7
X = np.column_stack((x1, x2, x3))
y = 1 + 0.2 * x1 + 0.5 * x2 + x3 + np.sin(2 * np.pi * x1)
return X, y
X, y = make_data()
#===================================================================
# Additive linear model and additive boosted trees
#===================================================================
# Linear model with polynomial terms
poly = PolynomialFeatures(degree=3, include_bias=False)
preprocessor = ColumnTransformer(
transformers=[
("poly0", poly, [0]),
("poly1", poly, [1]),
("other", "passthrough", [2]),
]
)
model_lm = Pipeline(
steps=[
("preprocessor", preprocessor),
("lm", LinearRegression()),
]
)
_ = model_lm.fit(X, y)
# Boosted trees with single-split trees
params = dict(
learning_rate=0.05,
objective="mse",
max_depth=1,
colsample_bynode=0.7,
)
model_lgb = lgb.train(
params=params,
train_set=lgb.Dataset(X, label=y),
num_boost_round=300,
)SHAP
For both models, we use exact permutation SHAP and exact Kernel SHAP. Furthermore, the linear model is analyzed with “additive SHAP”, and the tree-based model with TreeSHAP.
Do the algorithms provide the same?
system.time({ # 1s
shap_lm <- list(
add = shapviz(additive_shap(fit_lm, df)),
kern = kernelshap(fit_lm, X = df[xvars], bg_X = df),
perm = permshap(fit_lm, X = df[xvars], bg_X = df)
)
shap_lgb <- list(
tree = shapviz(fit_lgb, X),
kern = kernelshap(fit_lgb, X = X, bg_X = X),
perm = permshap(fit_lgb, X = X, bg_X = X)
)
})
# Consistent SHAP values for linear regression
all.equal(shap_lm$add$S, shap_lm$perm$S)
all.equal(shap_lm$kern$S, shap_lm$perm$S)
# Consistent SHAP values for boosted trees
all.equal(shap_lgb$lgb_tree$S, shap_lgb$lgb_perm$S)
all.equal(shap_lgb$lgb_kern$S, shap_lgb$lgb_perm$S)
# Linear coefficient of x3 equals slope of SHAP values
tail(coef(fit_lm), 1) # 1.112096
diff(range(shap_lm$kern$S[, "x3"])) # 1.112096
sv_dependence(shap_lm$add, xvars)sv_dependence(shap_lm$add, xvars, color_var = NULL)shap_lm = {
"add": shap.Explainer(model_lm.predict, masker=X, algorithm="additive")(X),
"perm": shap.Explainer(model_lm.predict, masker=X, algorithm="exact")(X),
"kern": shap.KernelExplainer(model_lm.predict, data=X).shap_values(X),
}
shap_lgb = {
"tree": shap.Explainer(model_lgb)(X),
"perm": shap.Explainer(model_lgb.predict, masker=X, algorithm="exact")(X),
"kern": shap.KernelExplainer(model_lgb.predict, data=X).shap_values(X),
}
# Consistency for additive linear regression
eps = 1e-12
assert np.abs(shap_lm["add"].values - shap_lm["perm"].values).max() < eps
assert np.abs(shap_lm["perm"].values - shap_lm["kern"]).max() < eps
# Consistency for additive boosted trees
assert np.abs(shap_lgb["tree"].values - shap_lgb["perm"].values).max() < eps
assert np.abs(shap_lgb["perm"].values - shap_lgb["kern"]).max() < eps
# Linear effect of last feature in the fitted model
model_lm.named_steps["lm"].coef_[-1] # 1.112096
# Linear effect of last feature derived from SHAP values (ignore the sign)
shap_lm["perm"][:, 2].values.ptp() # 1.112096
shap.plots.scatter(shap_lm["add"])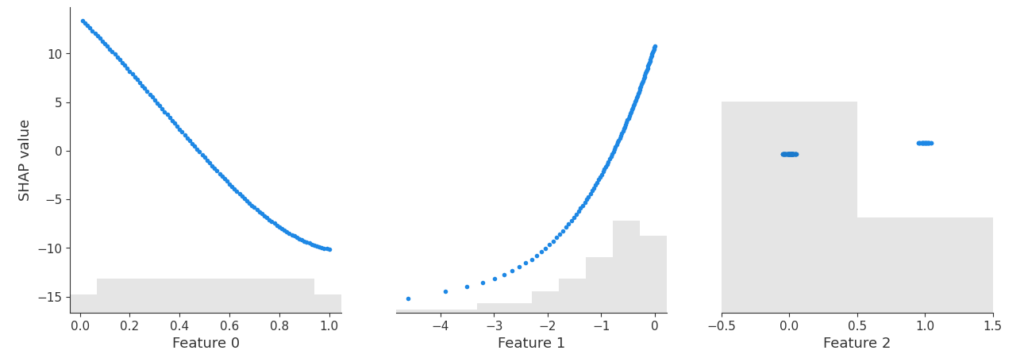
Yes – the three algorithms within model provide the same SHAP values. Furthermore, the SHAP values reconstruct the additive components of the features.
Didactically, this is very helpful when introducing SHAP as a method: Pick a white-box and a black-box model and compare their SHAP dependence plots. For the white-box model, you simply see the additive components, while the dependence plots of the black-box model show scatter due to interactions.
Remark: The exact equivalence between algorithms is lost, when
- there are too many features for exact procedures (~10+ features), and/or when
- the background data of Kernel/Permutation SHAP does not agree with the training data. This leads to slightly different estimates of the baseline value, which itself influences the calculation of SHAP values.
Final words
- SHAP algorithms applied to additive models typically give identical results. Slight differences might occur because sampling versions of the algos are used, or a different baseline value is estimated.
- The resulting SHAP values describe the additive components.
- Didactically, it helps to see SHAP analyses of white-box and black-box models side by side.
Leave a Reply